【最小生成树】学习笔记
【最小生成树】学习笔记
shy_lihui
·
2025-03-30 13:36:03
·
算法·理论
本文中,为了避免歧义,定义:
前置知识
树
并查集
生成树
理论
最小生成树是指边权和最小的生成树,\text{(Minimum Spanning Tree,MST)}。
比如这个图:
它的最小生成树是:
权值之和为 15。
并且没有方案使得其他生成树权值之和比 15 小。
这个树,就是最小生成树。
最小生成树的常见算法有两种:\text{kruskal} 和 \text{prim} 算法。
kruskal
算法实现
- 定义最小生成树是一个空集。
- 找到一条权值最短的边。
- 判断加入此边会不会出现环。
- 会:回到第二步
- 不会:加入集合,删除此边,回到第二步。
判断联通性可以使用[并](https://www.luogu.com.cn/article/yarkuugt)[查](https://blog.csdn.net/bjweimengshu/article/details/108332389)[集](https://www.bilibili.com/video/BV1ge4y1b78w)维护。
## 时间复杂度分析
并查集的路径压缩和启发式合并就把处理变的时间复杂度降维到了 $\text{O}(m)$,时间花费最大的是排序,用快速排序整体代码的时间复杂度为 $\text{O}(m \log m)$。
如果边权小的话可以直接计数排序就是 $\text{O}(m+W)$($W$ 表示边权最大值)。
## 举例
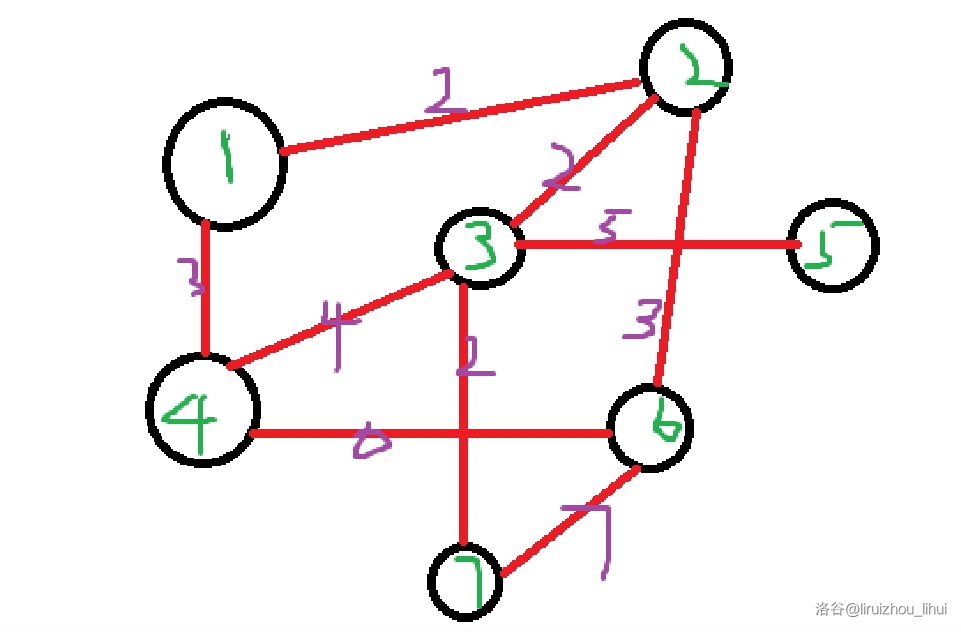
那么用 $\text{kruskal}$ 算法求最小生成树的过程为:
- 当前 $1 \leftrightarrow 2$ 的边权最小,加入不会出现环,将 $1 \leftrightarrow 2$ 加入集合。当前权值之和:$2$。
- 当前 $2 \leftrightarrow 3$ 的边权最小,加入不会出现环,将 $2 \leftrightarrow 3$ 加入集合。当前权值之和:$2+2=4$。
- 当前 $3 \leftrightarrow 7$ 的边权最小,加入不会出现环,将 $3 \leftrightarrow 7$ 加入集合。当前权值之和:$4+2=6$。
此时,权值为 $2$ 的所有边已经操作完成,图变成了这样:
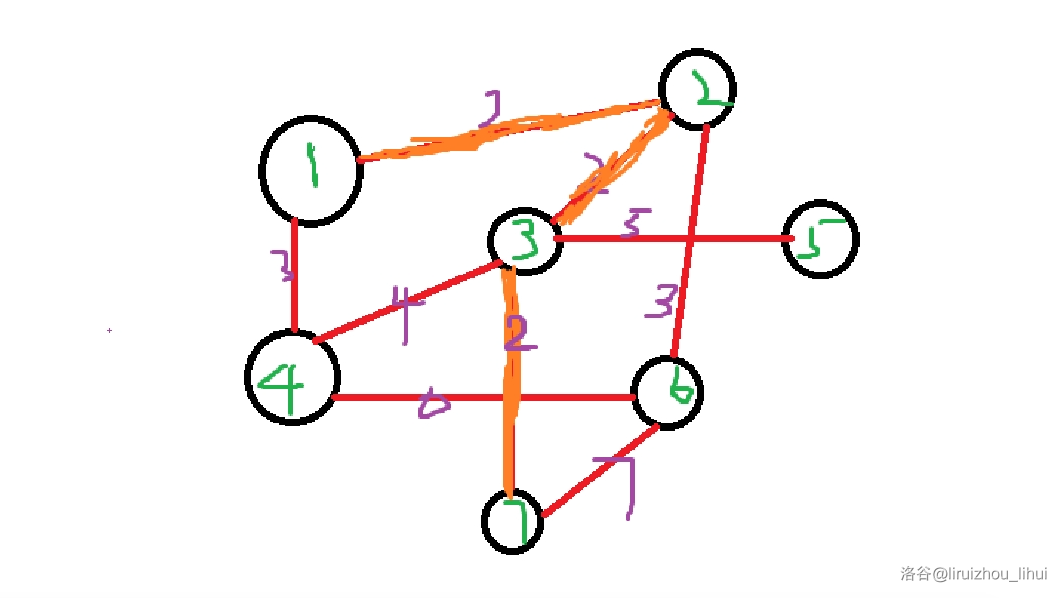
我们用刚才的办法操作所有的边权为 $3$ 的点,也不会有环,操作后图变成了:
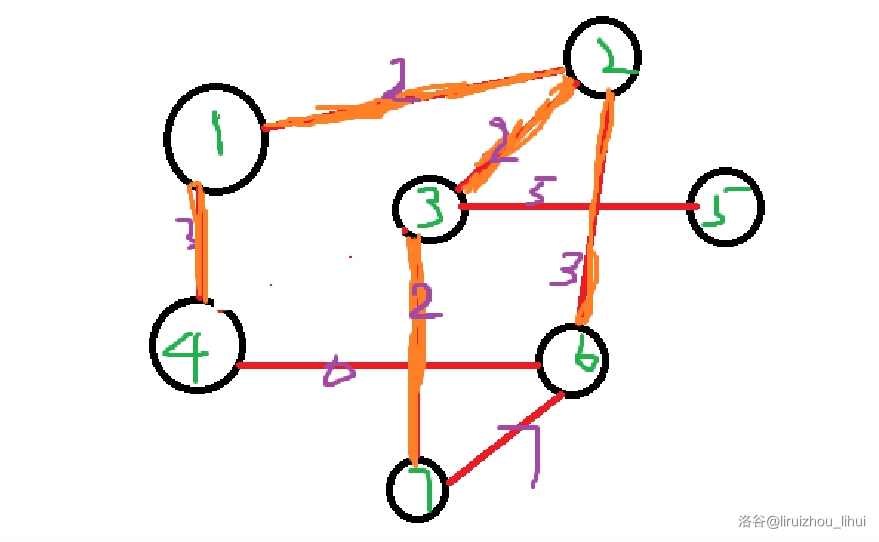
权值之和为 $12$。
- 当前 $3 \leftrightarrow 4$ 的边权最小,加入**会**出现环,删掉。
此时,权值为 $4$ 的所有边已经操作完成,图变成了这样:

- 当前 $3 \leftrightarrow 5$ 的边权最小,加入不会出现环,将 $3 \leftrightarrow 5$ 加入集合。当前权值之和:$12+5=17$。
- 当前 $4 \leftrightarrow 6$ 的边权最小,加入**会**出现环,删掉。
- 当前 $6 \leftrightarrow 7$ 的边权最小,加入**会**出现环,删掉。
现在所有的点已经被操作完成,图为:

这个就是它的最小生成树。
## 代码
用 P3366 举例。
先按照边权为第一关键字排序,再便利每次把边进行操作。连通性可以用并查集维护。使用路径压缩和启发式合并。最后判断联通直接看 $cnt_{\operatorname{findfa}(x)}$ 是否等于 $n$ 即可。
$cnt_i$ 是指 $i$ 为根的树的结点数量。
```cpp
#include
using namespace std;
const int MAXN=5000;
const int MAXM=2e5;
int n,m,sum;
int fa[MAXN+5];
int cnt[MAXN+5];
int findfa(int x)
{
if(fa[x]==x)
{
return x;
}
return fa[x]=findfa(fa[x]);
}
struct node
{
int u,v,w;
}e[MAXM+5];
bool cmp(node x,node y)
{
return x.w } int main() { ios::sync_with_stdio(0); cin.tie(0); cin>>n>>m; for(int i=1;i<=m;i++) { cin>>e[i].u>>e[i].v>>e[i].w; } for(int i=1;i<=n;i++) { fa[i]=i; cnt[i]=1; } sort(e+1,e+1+m,cmp); for(int i=1;i<=m;i++) { int u=e[i].u; int v=e[i].v; int w=e[i].w; int fau=findfa(u); int fav=findfa(v); if(fau==fav) { continue; } if(cnt[fau]>cnt[fav]) { cnt[fau]+=cnt[fav]; fa[fav]=fa[u]; } else { cnt[fav]+=cnt[fau]; fa[fau]=fa[v]; } sum+=w; } if(cnt[findfa(1)]==n) { cout< } else { cout<<"orz"; } return 0; } ``` ## 正确性证明 为了造出一棵最小生成树,显然是有 $n-1$ 条边。 用反证法证明: 生成的生成树 T 不是 $\text{MST}$,存在另一个生成树 $T'$,满足 $\operatorname{w}(T')<\operatorname{w}(T)$。 设 $e$ 为 $T$ 中存在且 $T'$ 不存在的最小边权,$e$ 是按权值从小到大选择且不形成环的边。 将 $e$ 加入 $T'$ 会出现环,此环中必有一条边 $f$ 属于 $T'$ 但不属于 $T$。 由于 $e$ 是差异边中权值最小的,因为会优先选择最小权边,故 $\operatorname{w}(f) \ge \operatorname{w}(e)$。 将 $T'$ 中的 $f$ 替换为 $e$,得到新生成树 $T''$,满足 $w(T'')=w(T')-w(f)+w(e)\le w(T ')$。这与 $T'$ 是最小生成树矛盾。 # prim ## 算法实现 $\operatorname{prim}$ 算法也可以求最小生成树,相对于 $\operatorname{kruskal}$ 比较麻烦且时间复杂度相同。但有的题目无法使用 $\operatorname{kruskal}$ 解决,$\operatorname{prim}$ 仍是很重要的算法。 $\operatorname{prim}$ 算法的思想类似于 $\operatorname{dijkstra}$,每次处理边的最小权值。 $\operatorname{prim}$ 算法的实现过程: - 从一个特定的节点 $s$ 开始,将所有与 $s$ 相连的边以权重从小到大放入优先队列;如果权重相同,则根据节点的序号。 - 如果在优先队列中最前面的边 $u\leftrightarrow v$ 中的 $v$ 还没有被访问过,那么我们可以包括 $v$ 来扩展最小生成树并将 $v$ 的边排进优先队列中;否则放弃这条边。不然会出现环。 - 回到第二步,直到最小生成树被构造出来 实际上可以每次跑一遍最大值不需要优先队列。 ## 时间复杂度分析 如果是稀疏图用优先队列优化可以达到 $\text{O}( m\log n)$ 的速度。 如果是稠密图需要每次跑一遍最大值而不应使用优先队列,因为 $m$ 最大是 $\frac{n(n-1)}{2}$,用堆优化可能退化到 $\text{O}(n^3)$,直接暴力找可以直接达到 $\text{O}(n^2)$. ## 举例 (本示例中蓝色边表示未处理的边,绿色的边表示在队列里的边,橙色的边表示最小生成树的边,被擦去的边表示不是最小生成树的边。) 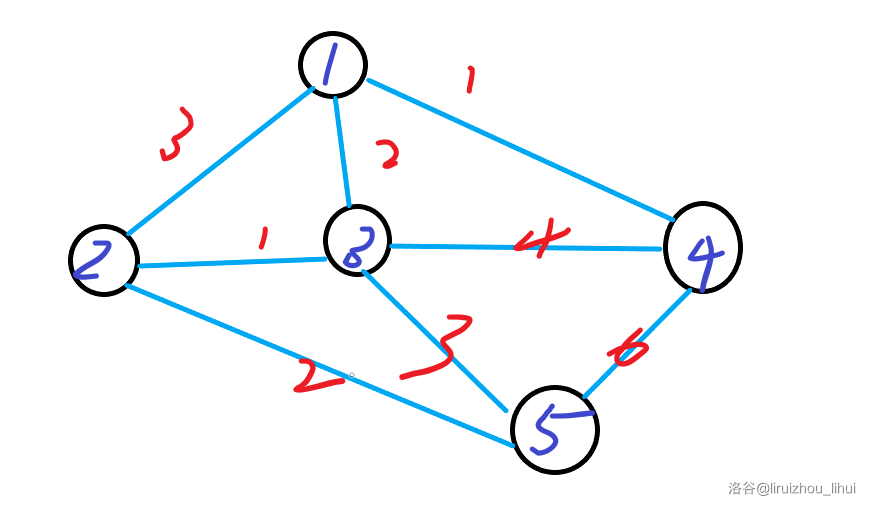 求最小生成树的过程为: - 将 $1$ 加入已选定集合 $E=\{1\}$。 - 把和 $1$ 有关的边放入优先队列。 - 此时队列中队首(即边权的最小值)为 $1(1\leftrightarrow 4)$,且没有操作过,选择这条边。此边出队。 - 将 $4$ 加入已选定集合 $E=\{1,4\}$。 - 把和 $4$ 有关的边放入优先队列。 操作后的图变成了这样:  - 此时队列中队首(即边权的最小值)为 $2(1\leftrightarrow 3)$,且没有操作过,选择这条边。此边出队。 - 将 $3$ 加入已选定集合 $E=\{1,3,4\}$。 - 把和 $3$ 有关的边放入优先队列。 此时的图:  - 此时队列中队首(即边权的最小值)为 $1(2\leftrightarrow 3)$,且没有操作过,选择这条边。此边出队。 - 将 $3$ 加入已选定集合 $E=\{1,2,3,4\}$。 - 因为所有边全部入队,所以无需继续把新的边压入队列。 此时的图:  - 此时队列中队首(即边权的最小值)为 $2(2\leftrightarrow 5)$,且没有操作过,选择这条边。此边出队。 - 将 $5$ 加入已选定集合 $E=\{1,2,3,4,5\}$。 - 因为所有边全部入队,所以无需继续把新的边压入队列。 因为现在的 $E$ 集合已满所以最小生成树已经成形,保留所有的橙色边后最小生成树就是:  --- 显然我刚才的示例的数据比较垃圾没有出现环的情况。但是有环也很好解决,直接看这条边之前处理过没有即可。 ## 代码 按照 P3366 来说。 ```cpp #include using namespace std; priority_queue const int INF=1e9; struct node { int v,w; }; int n,m; vector int dis[10005];//从起点到其他各个点的距离 bool vis[10005];//某个点是否已经加入生成树 int main() { ios::sync_with_stdio(0); cin.tie(0); cin>>n>>m; for(int i=1;i<=m;i++) { int u,v,w; cin>>u>>v>>w; edge[u].push_back({v,w}); edge[v].push_back({u,w}); // 由于是无向图,所以要将另一条边也加入邻接表中 } for(int i=1;i<=n;i++)//初始化 { dis[i]=INF; vis[i]=0; } dis[1]=0; pq.push(make_pair(0,1)); int ans=0; while(!pq.empty()) { int u=pq.top().second; pq.pop(); if(vis[u]) { continue;//如果u已经被访问过,则跳过 } vis[u]=true;//将u标记为已访问 for(int i=0;i { int v=edge[u][i].v; int w=edge[u][i].w; if (!vis[v] && w { dis[v]=w; pq.push(make_pair(dis[v],v)); } } ans+=dis[u]; } for(int i=1;i<=n;i++) { if(vis[i]==0) { cout<<"orz"; return 0; } } cout< return 0; } ``` ## 正确性证明 还是反证法 假设:设此算法求出的 $T$ 不是最小生成数,存在另一个生成树 $T'$,满足 $\operatorname{w}(T') < \operatorname{w}(T)$ 。 设 $e$ 是第一个被加入 $T$ 但不在 $T'$ 中的边。此时,$e$ 连接已选顶点集合 $E$ 和未选集合 $E'$ 。 $T'$ 必须包含一条边 $f$ 连接 $E$ 和 $E'$ ,否则 $T'$ 不连通。 因为 $e$ 是连接 $E$ 和 $E'$ 的最小权边,故 $\operatorname{w}(e) \le \operatorname{w}(f)$。 若 $\operatorname{w}(f) < \operatorname{w}(e)$,则应优先选择 $f$,与算法规则矛盾。因此 $T'$ 不存在。 假设不成立,所以 $T$ 最小生成树。 # Borůvka ## 算法实现 在稠密图上不如 ${\operatorname{prim}}$,稀疏图上逊于 $\operatorname{kruskal}$,只适用于求**完全图**的最小生成树,但实际上没啥用,主流的两个算法也能求完全图。在朋友面前装装还行。 $\operatorname{kruskal}$ 和 ${\operatorname{prim}}$ 缝合到一起就是 $\operatorname{Borůvka}$ 算法。 $\operatorname{Borůvka}$ 算法的本质是多源 ${\operatorname{prim}}$。 实现步骤如下: - 每个点先看成只有根的树。 - 找到每个森林的临边最小权值。 - 如果加入出现环则跳过。 - 没有环就加入这条边让两个树合并成一个树。 - 回到第二部直到最小生成树确定。 用了 ${\operatorname{prim}}$ 的贪心策略,结合了$\operatorname{kruskal}$ 的并查集,就出了这个算法。 ## 时间复杂度分析 注意到每次进行操作二的时候,找最小值需要 $\text{O}(m)$,所以森林进行一次合并操作就是 $\text{O}(m) 每次都会把两个树合并为一个树所以合并次数为 \log n。 综合下来就是 \text{O}(m \log n)。 举例 这里用 OIwiki 的示例来说。 模拟过程: 此时剩下两个树,合并 E\leftrightarrow J。 所有边均被处理,\operatorname{Borůvka} 算法结束。 虽然不知道为什么原动图上 E 和 J 没有边。没边不就是最小生成森林了吗,再且如果就是求的是森林还不如每个节点是一个独根树和为 0。 代码 还是 P3366。 #include #include #include using namespace std; const int MAXN=5000; const int MAXM=200000; int n,m; int u[MAXM+5],v[MAXM+5],w[MAXM+5]; bool used[MAXM+5]; int fa[MAXN+5],Best[MAXN+5]; int findfa(int x) { if(x==fa[x]) { return x; } return fa[x]=findfa(fa[x]); } bool cmp(int x,int y) { if(y==0) { return 1; } if(w[x]!=w[y]) { return w[x] } return x } void Boruvka() { for(int i=1;i<=n;i++) { fa[i]=i; } int cnt=0,sum=0; bool flag=1; while(flag) { flag=0; memset(Best,0,sizeof Best); for(int i=1;i<=m;i++) { int U=u[i]; int V=v[i]; int W=w[i]; if(used[i]==1) { continue; } int fau=findfa(u[i]); int fav=findfa(v[i]); if(fau==fav) { continue; } if(cmp(i,Best[fau])==1) { Best[fau]=i; } if(cmp(i,Best[fav])==1) { Best[fav]=i; } } for(int i=1;i<=n;i++) { if(Best[i]!=0&&used[Best[i]]==0) { flag=1; cnt++; sum+=w[Best[i]]; used[Best[i]]=1; fa[findfa(u[Best[i]])]=findfa(v[Best[i]]); } } } if(cnt==n-1) { cout< } else { cout<<"orz"; } } int main() { ios::sync_with_stdio(0); cin.tie(0); cin>>n>>m; for(int i=1;i<=m;++i) { cin>>u[i]>>v[i]>>w[i]; } Boruvka(); return 0; } 正确性证明 假设 \operatorname{Borůvka} 算法生成的生成树 T 不是最小生成树。根据反证法,存在另一个生成树 T' 满足 \operatorname w(T') < \operatorname w(T)。 考虑 \operatorname{Borůvka} 算法执行过程中第一次选择一条不在 T' 中的边 e 的时刻。 设此时算法处理的树为 x 和 y,且 e 是连接 x 和 y 的最小权边。 由于 T' 是生成树,它必须包含连接 x 和 y 的某条边 f。 那么,有: \operatorname w(e) \le \operatorname w(f)。 否则,会在该步骤中选择 f 而非 e ,与假设矛盾。 将 T' 中的边 f 替换为 e,得到新生成树。 此时:\operatorname w(T'') = \operatorname w(T') - \operatorname w(f) + \operatorname w(e) \le \operatorname w(T') 但 T'' 的总权值不大于 T',这与 T' 是 \text{MST} 矛盾。因此,原假设不成立,故正确。 一些 \text{MST} 好题 P10928 走廊泼水节 大意就是给你一个最小生成树让你加一些边变成完全图,求完全图的权值最小值。 因为要使新增的权值最小,所以此时对于 u 连通块内到 v 连通块的边边权应该为 w+1,如果更小就会破坏原定的最小生成树。贡献和为 (s_u\times s_v-1)\times(w+1),s_i 表示 i 联通块的节点数量。 #include using namespace std; const int MAXN=6000; const int MAXM=5999; int n,sum; int fa[MAXN+5]; int cnt[MAXN+5]; int findfa(int x) { if(fa[x]==x) { return x; } return fa[x]=findfa(fa[x]); } struct node { int u,v,w; }e[MAXM+5]; bool cmp(node x,node y) { return x.w } int t; int main() { ios::sync_with_stdio(0); cin.tie(0); cin>>t; while(t--) { cin>>n; for(int i=1;i { cin>>e[i].u>>e[i].v>>e[i].w; } for(int i=1;i<=n;i++) { fa[i]=i; cnt[i]=1; } sum=0; sort(e+1,e+1+n-1,cmp); for(int i=1;i { int u=e[i].u; int v=e[i].v; int w=e[i].w; int fau=findfa(u); int fav=findfa(v); sum+=(cnt[fau]*cnt[fav]-1)*(w+1); if(cnt[fau]>cnt[fav]) { cnt[fau]+=cnt[fav]; fa[fav]=fa[u]; } else { cnt[fav]+=cnt[fau]; fa[fau]=fa[v]; } } cout< } return 0; } P1265 公路修建 因为边很多用堆优化反而更慢,每次直接暴力找最小值即可。 ```cpp #include #define int long long using namespace std; const int MAXN=5000; int n,m; int x[MAXN+5],y[MAXN+5]; vector double dis[MAXN+5]; bool vis[MAXN+5]; double len(int i,int j) { return sqrt((int)(x[i]-x[j])*(x[i]-x[j])+ (int)(y[i]-y[j])*(y[i]-y[j])); } signed main() { ios::sync_with_stdio(false); cin.tie(0); cin>>n; for(int i=1;i<=n;i++) { cin>>x[i]>>y[i]; } for(int i=1;i<=n;i++) { dis[i]=1e12,vis[i]=0; } dis[1]=0; double sum=0; for(int i=1;i<=n;i++) { int u=-1; for(int i=1;i<=n;i++) { if(!vis[i]&&(u==-1||dis[i] { u=i; } } vis[u]=1; sum+=dis[u]; for(int v=1;v<=n;v++) { if(len(u,v) { dis[v]=len(u,v); } } } cout< return 0; } ``` ## [P4047 [JSOI2010] 部落划分](https://www.luogu.com.cn/problem/P4047) 每次找最近的两个部落把他们合并是最优的。 最后剩下 $k$ 个部落的时候当前处理到的边(加入不联通)就是目标距离。 我用的 $\operatorname{kruskal}$ 和优先队列。 ```cpp #include using namespace std; int n,k; struct node { int x,y; double w; bool operator<(const node x)const { return w>x.w; } }; double slove(int x,int y,int xx,int yy) { return sqrt(double((x-xx)*(x-xx)+(y-yy)*(y-yy))); } priority_queue int U[1005]; int V[1005]; int fa[10000*10000+10000]; int findfa(int x) { if(fa[x]==x) { return x; } return fa[x]=findfa(fa[x]); } int main() { ios::sync_with_stdio(0); cin.tie(0); cin>>n>>k; for(int i=1;i<=n;i++) { cin>>U[i]>>V[i]; } for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(i==j||i>j) { continue; } q.push({i,j,slove(U[i],V[i],U[j],V[j])}); } } for(int i=1;i<=n;i++) { fa[i]=i; } int sum=n; while(sum>k) { //cout< node x=q.top(); q.pop(); int u=x.x; int v=x.y; int fau=findfa(u); int fav=findfa(v); if(fau!=fav) { fa[fau]=fav; sum--; } } while(1) { node x=q.top(); q.pop(); int u=x.x; int v=x.y; int fau=findfa(u); int fav=findfa(v); if(fau!=fav) { printf("%.2lf",x.w); return 0; } } return 0; } ``` ## [P1550 [USACO08OCT] Watering Hole G](https://www.luogu.com.cn/problem/P1550) 对于一个田,要让其有水,有两种办法:挖井,引水入田。 可以定一个特殊点 $s$,$s$ 连向每块田,权值为开凿水井的话费。 这样 $n+1$ 个点,$n+m$ 条边,跑一个最小生成树即可。 ```cpp #include using namespace std; const int MAXN=600; int n,m,sum,flag=1; int fa[MAXN+5]; int cnt[MAXN+5]; int findfa(int x) { if(fa[x]==x) { return x; } return fa[x]=findfa(fa[x]); } struct node { int u,v,w; }; vector bool cmp(node x,node y) { return x.w } int main() { ios::sync_with_stdio(0); cin.tie(0); cin>>n; for(int i=1;i<=n;i++) { int w; cin>>w; e.push_back({0,i,w}); } for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { int p; cin>>p; if(i==j || i>j) { continue; } e.push_back({i,j,p}); } } for(int i=0;i<=n;i++) { fa[i]=i; cnt[i]=1; } sort(e.begin(),e.end(),cmp); for(int i=0;i { int u=e[i].u; int v=e[i].v; int w=e[i].w; int fau=findfa(u); int fav=findfa(v); if(fau==fav) { continue; } if(cnt[fau]>cnt[fav]) { cnt[fau]+=cnt[fav]; fa[fav]=fa[u]; } else { cnt[fav]+=cnt[fau]; fa[fau]=fa[v]; } sum+=w; } cout< return 0; } ``` ## [P1396 营救](https://www.luogu.com.cn/problem/P1396) Don't open the door for strangers. 正常搞 $\operatorname{kruskal}$ 就行了,如果遇到加边成环就输出此边的权值。 因为之前的所有边权都小于等于当前边权,所以当前边权是这条路径的最大边权。由于我们是按从小到大加入的,任何其他路径的最大边权不可能比这个小(否则会出现环)。 ```cpp #include using namespace std; const int MAXN=1e4; const int MAXM=2e4; int n,m,s,t; int fa[MAXN+5]; int cnt[MAXN+5]; int findfa(int x) { if(fa[x]==x) { return x; } return fa[x]=findfa(fa[x]); } struct node { int u,v,w; }e[MAXM+5]; bool cmp(node x,node y) { return x.w } int main() { ios::sync_with_stdio(0); cin.tie(0); cin>>n>>m>>s>>t; for(int i=1;i<=m;i++) { cin>>e[i].u>>e[i].v>>e[i].w; } for(int i=1;i<=n;i++) { fa[i]=i; cnt[i]=1; } sort(e+1,e+1+m,cmp); for(int i=1;i<=m;i++) { int u=e[i].u; int v=e[i].v; int w=e[i].w; int fau=findfa(u); int fav=findfa(v); if(fau==fav) { continue; } if(cnt[fau]>cnt[fav]) { cnt[fau]+=cnt[fav]; fa[fav]=fa[u]; } else { cnt[fav]+=cnt[fau]; fa[fau]=fa[v]; } if(findfa(s)==findfa(t)) { cout< return 0; } } return 0; } ``` # 后记 ~~$\sout{\operatorname{kruskal}}$ 但是用优先队列有种屁股得了关节炎的感觉。~~ $\operatorname{kruskal}$ 和 $\operatorname{prim}$ 都是很重要的算法。 至于 $\operatorname{Borůvka}$ 是不会在 NOI 赛事中出现的,仅限于大纲更改之前。 --- 有没有更强势还吃操作的最小生成树算法呢?[有的兄弟,有的。](https://www.cs.princeton.edu/~chazelle/pubs/mst.pdf)